• Markov Chain Monte Carlo methods
  • Metropolis Hastings
  • Gibbs
• convergence / representativeness
  • trace plots
  • R hat
• efficiency
  • autocorrelation
  • effective sample size

Bayes rule for data analysis:

\[\underbrace{P(\theta \, | \, D)}_{posterior} \propto \underbrace{P(\theta)}_{prior} \times \underbrace{P(D \, | \, \theta)}_{likelihood}\]

normalizing constant:

\[ \int P(\theta') \times P(D \mid \theta') \, \text{d}\theta' = P(D) \]

easy to solve only if:

• \(\theta\) is a single discrete variable with reasonably sized domain
• \(P(\theta)\) is conjugate prior for the likelihood function \(P(D \mid \theta)\)
• we are very lucky

# get density values and samples
xVec = seq(-4, 4, length.out = 10000)
xDense = dnorm(xVec, mean = 0, sd = 1) # density of a standard normal 
xSamples = rnorm(10000, mean = 0, sd = 1) # 10000 samples from a standard normal
# plot actual densities and estimated densities from samples
plotData = data.frame(xSamples = xSamples) # put data in data frame for plotting
myPlot = ggplot(data = plotData, aes(x = xSamples)) +  # prepare plot
  geom_density() + # density estimates
  geom_line(x = xVec, y = xDense, color = "blue") + # actual densities
  xlab("x") + ylab("(estimated) probability") + # axis labels
  theme(plot.background=element_blank()) # transparent background
show(myPlot)

• \(X = (X_1,\dots,X_k)\) is a vector of random variables
  • think \(\theta\), but here more generally any \(X\)
• \(x\) is a realization (or particular value) of \(X\)
• distribution of \(X\) is \(P\), to be written as \(X \sim P\)

examples:

• \(X \sim N(\mu,\sigma)\)
  • read: "\(X\) is normally distributed with mean \(\mu\) and SD \(\sigma\)"
• \(\theta \sim \text{beta}(a,b)\)
  • read: "\(\theta\) comes from a beta distribution with shape \(a\) and \(b\)"

problem:

• assume that \(X \sim P\) and that \(P\) is "unwieldy"
• we'd like to know: \(f(X)\)
  • e.g., mean/median/sd of \(X\), 95% HDI, \(\dots\)
  • or, marginalized distribution over \(X_i\)

dummy

solution:

• Monte Carlo simulation
  • draw samples \(S\) from \(P\)
  • calculate \(f(S)\)
  • for many \(f\), \(f(S)\) will approximate \(f(X)\) if \(S\) is "representative" of \(P\)

intuition

• a sequence of elements from \(X\), \(x_0, x_1, \dots, x_n\) such that every \(x_{i+1}\) depends only on its predecessor \(x_i\)
  • think: probabilistic finite state machine

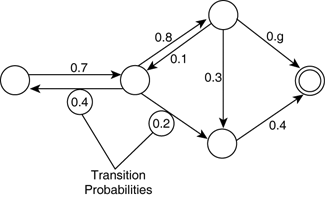
Markov property

\[P(X_{n+1} = x_{n+1} \mid X_0 = x_0, \dots, X_n = x_n) = P(X_{n+1} = x_n \mid X_n = x_n)\]

get sequence of samples from \(X \sim P\) s.t. every sample depends on its predecessor, such that:

1. the stationary distribution of the chain is \(P\)
2. ideally, only few steps are necessary to get representative samples of \(P\)

dummy

• bad: non-independence -> autocorrelation
• good: no need to bother with normalizing constant

• set of islands \(X = \{x_1, x_2, \dots x_n\}\)
• goal: hop around & visit every island \(x_i\) proportional to its population \(P(x_i)\)
  • think: "samples" from \(X \sim P\)
• problem: island hopper can remember at most 2 islands' population
  • think: we don't know the normalizing constant

• let \(f(x) = \alpha P(x)\) (e.g., unnormalized posterior)
• start at random \(x^0\), define probability \(P_\text{trans}(x^i \rightarrow x^{i+1})\) of going from \(x^{i}\) to \(x^{i+1}\)
  • proposal \(P_\text{prpsl}(x^{i+1} \mid x^i)\): prob. of considering jump to \(x^{i+1}\) from \(x^{i}\)
  • acceptance \(P_\text{accpt}(x^{i+1} \mid x^i)\): prob of making jump when \(x^{i+1}\) is proposed \[P_\text{accpt}(x^{i+1} \mid x^i) = \text{min} \left (1, \frac{f(x^{i+1})}{f(x^{i})} \frac{P_\text{prpsl}(x^{i} \mid x^{i+1})}{P_\text{prpsl}(x^{i+1} \mid x^i)} \right)\]
  • transition \(P_\text{trans}(x^i \rightarrow x^{i+1}) = P_\text{prpsl}(x^{i+1} \mid x^i) \times P_\text{accpt}(x^{i+1} \mid x^i)\)

• motto: always up, down with probability \(\frac{f(x^{i+1})}{f(x^{i})}\)
• ratio \(\frac{f(x^{i+1})}{f(x^{i})}\) means that we can forget about normalizing constant
• \(P_\text{trans}(x^i \rightarrow x^{i+1})\) defines transition matrix -> Markov chain analysis!
• for suitable proposal distributions:
  • stationary distribution exists (first left-hand eigenvector)
  • every initial condition converges to stationary distribution
  • stationary distribution is \(P\)

• Metropolis is a very general and versatile algorithm
• however in specific situations, other algorithms may be better applicable
• for example, if \(X=(X_1,\dots,X_k)\) is a vector of random variables and \(P(x)\) is a multidimensional distribution
• in such cases, the Gibbs sampler may be helpful
• basic idea: split the multidimensional problem into a series of simpler problems of lower dimensionality

• assume \(X=(X_1,X_2,X_3)\) and \(p(x)=P(x_1,x_2,x_3)\)
• start with \(x^0=(x_1^0,x_2^0,x_3^0)\)
• at iteration \(t\) of the Gibbs sampler, we have \(x^{i-1}\) and need to generate \(x^{i}\)
  • \(x_1^{i} \sim P(x_1|x_2^{i-1},x_3^{i-1})\)
  • \(x_2^{i} \sim P(x_2|x_1^{i},x_3^{i-1})\)
  • \(x_3^{i} \sim P(x_3|x_1^{i},x_2^{i})\)
• for a large \(n\), \(x^n\) will be a sample from \(P(x)\)
  • \(x^n_k\) will be a sample from \(P(x_k)\) (marginal distribution)

• Gibbs sampling can be more efficient than MH
• Gibbs needs samples from conditional posterior distribution
  • MH is more generally applicable
• preformance of MH depends on proposal distribution

clever software helps determine when/how to do Gibbs and how to tune MH's proposal function (next class)

convergence/representativeness

• we have samples from MCMC, ideally several chains
• in the limit, samples must be representative of \(P\)
• how do we know that our meagre finite samples are representative?

efficiency

• ideally, we'd like the shortest samples that are representative
• how do we measure that we have "enough" samples?

require('coda')
require('ggmcmc')

out = MH(f, 60000,2,10000) # this is the output of the program of Ex 4 in HW 2
                  # its an MCMC-list from 'coda' package: i.e., a list
                  # of MCMC-objects
show(summary(out))

## 
## Iterations = 1:50000
## Thinning interval = 1 
## Number of chains = 2 
## Sample size per chain = 50000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##           Mean      SD  Naive SE Time-series SE
## mu    0.004904 0.07475 0.0002364      0.0012889
## sigma 1.051322 0.05314 0.0001680      0.0008058
## 
## 2. Quantiles for each variable:
## 
##          2.5%     25%      50%    75%  97.5%
## mu    -0.1484 -0.0424 0.006156 0.0562 0.1471
## sigma  0.9537  1.0136 1.050294 1.0867 1.1619

out2 = ggs(out)  # cast the same information into a format that 'ggmcmc' uses
show(head(out2)) # this is now a data.frame

## Source: local data frame [6 x 4]
## 
##   Iteration Chain Parameter       value
##       (int) (int)    (fctr)       (dbl)
## 1         1     1        mu -0.01714470
## 2         2     1        mu -0.09520337
## 3         3     1        mu -0.09520337
## 4         4     1        mu -0.09520337
## 5         5     1        mu -0.09520337
## 6         6     1        mu -0.09520337

plot(out)

ggs_traceplot(out2)

EJ Wagenmakers:

• trace plots from multiple chains should look like:
  • caterpillars madly in love with each other

\(\hat{R}\)-statistics,

• a.k.a.:
  • Gelman-Rubin statistics
  • shrink factor
  • potential scale reduction factor
• idea:
  • compare variance within a chain to variance between chains
• in practice:
  • use software to compute it
  • aim for \(\hat{R} \le 1.1\) for all continuous variables

gelman.diag(out)

## Potential scale reduction factors:
## 
##       Point est. Upper C.I.
## mu             1       1.00
## sigma          1       1.01
## 
## Multivariate psrf
## 
## 1

ggs_Rhat(out2)

autocorr.plot(out)

ggs_autocorrelation(out2)

• intuition:
  • how many samples are "efficient, actual samples" if we strip off autocorrelation
• definition:

\[\text{ESS} = \frac{N}{ 1 + 2 \sum_{k=1}^{\infty} ACF(k)}\]

effectiveSize(out)

##       mu    sigma 
## 3365.707 4355.494

• read Kruschke Chapter 8 in preparation
• install JAGS
• hand in homework 2